Data

• Title: Simple transitive 2-representations of Soergel bimodules for finite Coxeter types
• Authors: Marco Mackaay, Volodymyr Mazorchuk, Vanessa Miemietz, Daniel Tubbenhauer and Xiaoting Zhang
• Status: Proc. Lond. Math. Soc. (3) 126 (2023), no. 5, 1585-1655. Last update: Sun, 12 Feb 2023 08:03:32 UTC
• ArXiv link: https://arxiv.org/abs/1906.11468
• ArXiv version = 0.99 published version
• LaTex Beamer presentation: Slides1, Slides2a (joint with Marco Mackaay Slides2b and Slides2c), Slides3a and companion Slides3b, Slides4 (joint with Vanessa Miemietz Notes), Slides5, Slides6, Slides7

Abstract

In this paper we show that Soergel bimodules for finite Coxeter types have only finitely many equivalence classes of simple transitive 2-representations and we complete their classification in all types but \(H_{3}\) and \(H_{4}\).

A few extra words

Classification problems are among the most important basic problems in mathematics. For example, classifying simple representations of Hecke algebras has played an important role in modern representation theory. The present paper is motivated by the problem of classifying simple transitive 2-representations of the 2-category \(\mathcal{S}\) of Soergel bimodules associated to a finite Coxeter group, which one can see as a categorification of the classification problem for Hecke algebras. We do not give a complete answer, but an almost complete answer:
First of all, the Classification Problem for \(\mathcal{S}\) can be reduced to that of certain subquotients \(\mathcal{S}_{\mathcal{H}}\). To do that, one uses the cell structure of \(\mathcal{S}\), which is the categorical analog of the Kazhdan-Lusztig cell structure of Hecke algebras. By apex reduction and \(\mathcal{H}\)-reduction, it suffices to solve the classification problem for some \(\mathcal{S}_{\mathcal{H}}\) instead of \(\mathcal{S}\).
By the results in this paper, the benefits turn out to be even bigger. Based on Elias and Williamson's results, there exists a fusion bicategory \(\mathcal{A}_{\mathcal{H}}\), which categorifies the corresponding asymptotic Hecke algebra. The main insight of this paper is that these asymptotic bicategories completely determine the (graded) simple transitive 2-representations of \(\mathcal{S}\). To be precise, our main result is the existence of a biequivalence of categories of simple transitive 2-representations of \(\mathcal{S}_{\mathcal{H}}\) and \(\mathcal{A}_{\mathcal{H}}\).
Since \(\mathcal{A}_{\mathcal{H}}\) is semisimple and well-understood in the great majority of cases, the upshot is that the classification boils down to certain computational data; which in almost all cases is enough to parameterize the simple transitive 2-representations of \(\mathcal{S}\). Here is an example how such computational data might look like.

This is the cell structure of Coxeter type \(H_4\). In this case, which we barely understand, there would be still work to be done - even assuming our conjecture to be true. For example, we do not know what the asymptotic 2-categories for the big cell are - we only know its numerical data (e.g. Fusion graph, Perron-Frobenius dimensions as illustrated).
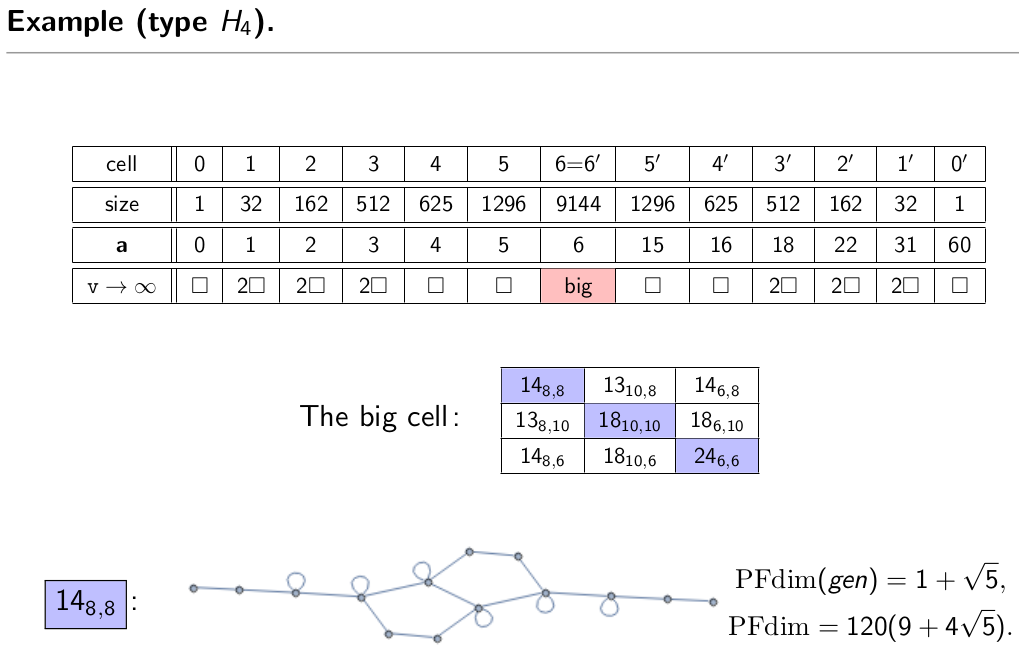
However, assuming our conjecture, types \(H_3\) and \(H_4\) are the only types which would remain open. That is, in all other types our conjecture would give a full classification of 2-simples.