Data
- Title: Cellularity and subdivision of KLR and weighted KLRW algebras
- Authors: Andrew Mathas and Daniel Tubbenhauer
- Status: Math. Ann. 389, 3043-3122 (2024). Last update: Fri, 19 Jan 2024 23:08:34 UTC
- ArXiv link: https://arxiv.org/abs/2111.12949
- ArXiv version = 0.99 published version
- Some idempotents plus code: C2 as pdf, C2 as tex, C3 as pdf, C3 as tex, C4 as pdf, C4 as tex
- LaTex Beamer presentation: Slides1, Slides2, Slides3, Slides4, Slides5
Abstract
Weighted KLRW algebras are diagram algebras generalizing KLR algebras. This paper undertakes a systematic study of these algebras culminating in the construction of homogeneous affine cellular bases in affine types \(A\) and \(C\), which immediately gives cellular bases for the cyclotomic quotients of these algebras. In addition, we construct subdivision homomorphisms that relate weighted KLRW algebras for different quivers. As an application we obtain new results about the (cyclotomic) KLR algebras of affine type, including (re)proving that the cyclotomic KLR algebras of type \(A^{(1)}_{e}\) and \(C^{(1)}_{e}\) are graded cellular algebras.
A few extra words
Khovanov-Lauda and independently Rouquier introduced the so-called
KLR algebras (or quiver Hecke algebras), motivated by questions in categorification,
or more precisely from categorical actions of Lie algebras and the categorification of
their simple highest weight modules. Webster further generalized these algebras to KLRW algebras, which give
categorifications of tensor products of simple highest weight modules. All of these algebras admit finite dimensional
quotients, called cyclotomic KLR(W) algebras. All of these algebras are graded algebras and all
can be defined diagrammatically using generators and relations.
Almost by definition, they play a crucial role in categorification and representation theory.
The discovery of these algebras and their properties started a major paradigm shift
in representation theory. As important special cases these algebras include
the group algebras of the symmetric group, its Hecke algebra, and the cyclotomic
Hecke algebras of type A. The KLR algebras revealed deep new structures in their modules.
To define the weighted KLRW algebras Webster embellished the KLR algebras
by introducing a weighting and additional strings to the diagrammatic presentation
of the KLR algebras, and some subtle changes in the relations.
Here is an example of how the diagrams look like:
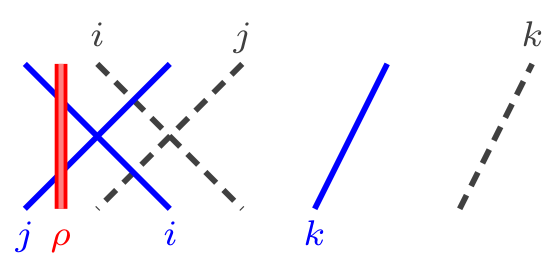
This paper undertakes a systematic study of these algebras.
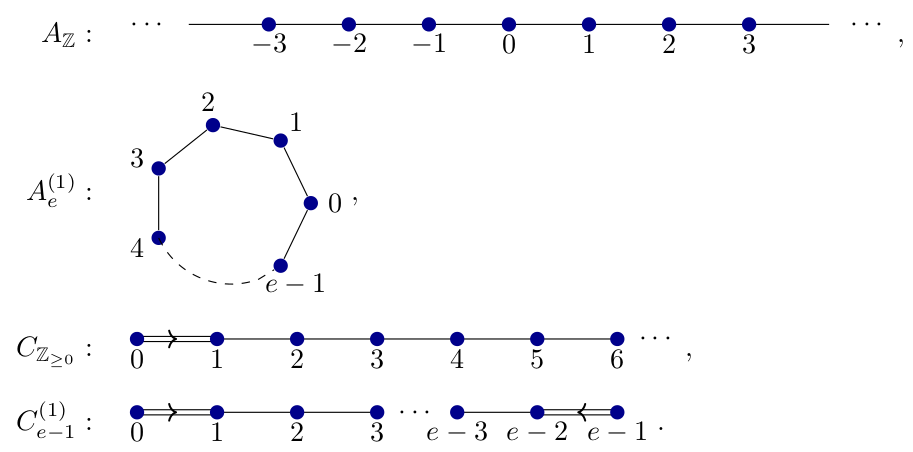
The earlier sections of this paper apply with almost no restrictions on the choice of quiver but for the some results of the paper we restrict our attention to the quivers: