Data

• Title: Tensor powers of representations of (diagram) monoids
• Authors: David He and Daniel Tubbenhauer
• Status: preprint. Last update: Wed, 6 Aug 2025 03:27:04 UTC
• Code and (possibly empty) Erratum: Click
• ArXiv link: http://arxiv.org/abs/2508.04054

Abstract

We study tensor powers of representations of finite monoids, focusing on the growth behavior of their composition length and the number of indecomposable summands. Special attention is given to diagram monoids such as the Temperley--Lieb, Motzkin, and Brauer monoids. For these examples, we compute explicit data, including some character tables, and analyze patterns in the decomposition of their tensor powers.

A few extra words

Here are the main objects under study:

Let \(C\) be an additive Krull–Schmidt monoidal category. Let \(X\in C\) be an object of \(C\). We define \[ b_{n}=b_{n}^{C,X}:=\#\text{indecomposable summands in \(X^{\otimes n}\) counted with multiplicities}. \] We identify the sequence \(b_{n}\) with its function \(n\mapsto b_{n}\). In the abelian setting, there is a similar definition for the length \(l_n\), that we will also use
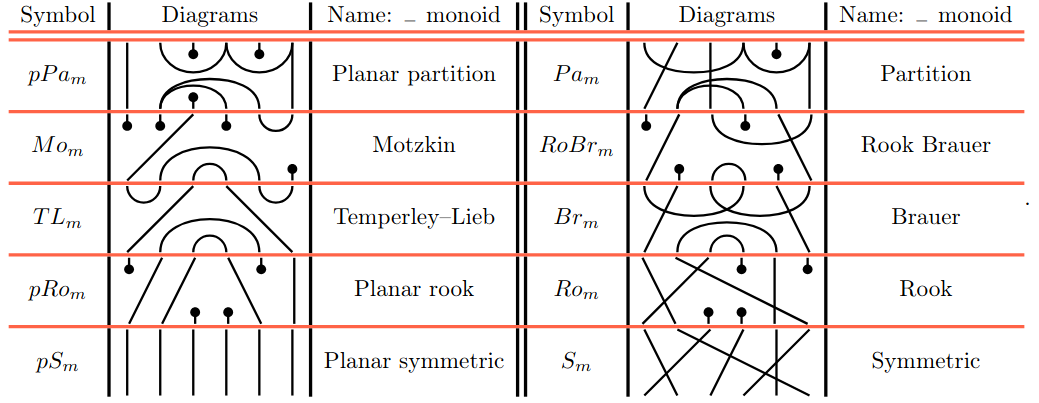
The functions \(l_n,b_{n}\) have been the subject of extensive study. In this paper we study them for monoids, in particular for diagram monoids as above.