Homepage Daniel Tubbenhauer - research paper Fractal behavior of tensor powers of the two dimensional space in prime characteristic

Data

Title: Fractal behavior of tensor powers of the two dimensional space in prime characteristic
Authors: Kevin Coulembier, Pavel Etingof, Victor Ostrik and Daniel Tubbenhauer
Status: preprint. Last update: Mon, 27 May 2024 03:17:22 UTC
ArXiv link: https://arxiv.org/abs/2405.16786

Abstract

We study the number of indecomposable summands in tensor powers of the vector representation of SL2. Our main focus is on positive characteristic where this sequence of numbers and its generating function show fractal behavior akin to Mahler functions.

A few extra words

For a group (scheme) $G$ and a finite dimensional (rational) $G$-representation $V$ let $b_n=b_n(V)$ denote the number of indecomposable summands of $V^{\otimes n}$, and $l_n=l_n(V)$ the length of $V^{\otimes n}$. We make the Ansatz that: we have \[ b_n\sim h(n)\cdot n^{a}\cdot(\dim V)^{n},\quad\mbox{and}\quad l_n\sim h'(n)\cdot n^{a'}\cdot(\dim V)^{n} \] for bounded functions $h$ and $h'$ and $a,a'\in\mathbb{R}$.
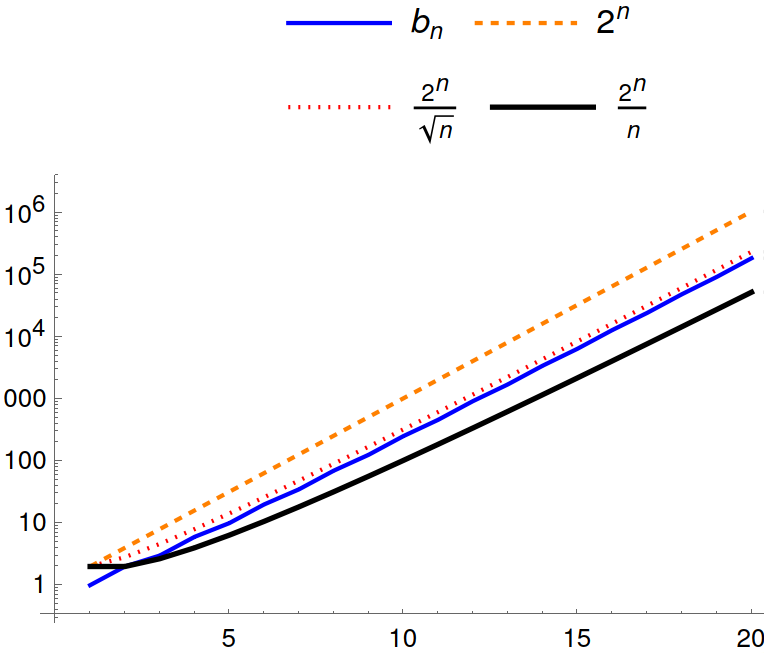
For example, take the vector representation $V=\mathbb{C}^2$ of $\mathrm{SL}_{2}(\mathbb{C})$, and let $b_n$ be the length of (equivalently the number of indecomposable summands in) $V^{\otimes n}$. One sees that $C\cdot n^{-1}\cdot 2^n\leq b_n\leq 2^n,C\in\mathbb{R}_{>0}$, since the largest possible summand in $V^{\otimes n}$ has dimension $n+1$, while $\dim V^{\otimes n}=2^n$. In fact, $b_n\sim a_n=D\cdot n^{-1/2}\cdot 2^n$, where $D=\sqrt{2/\pi}$. 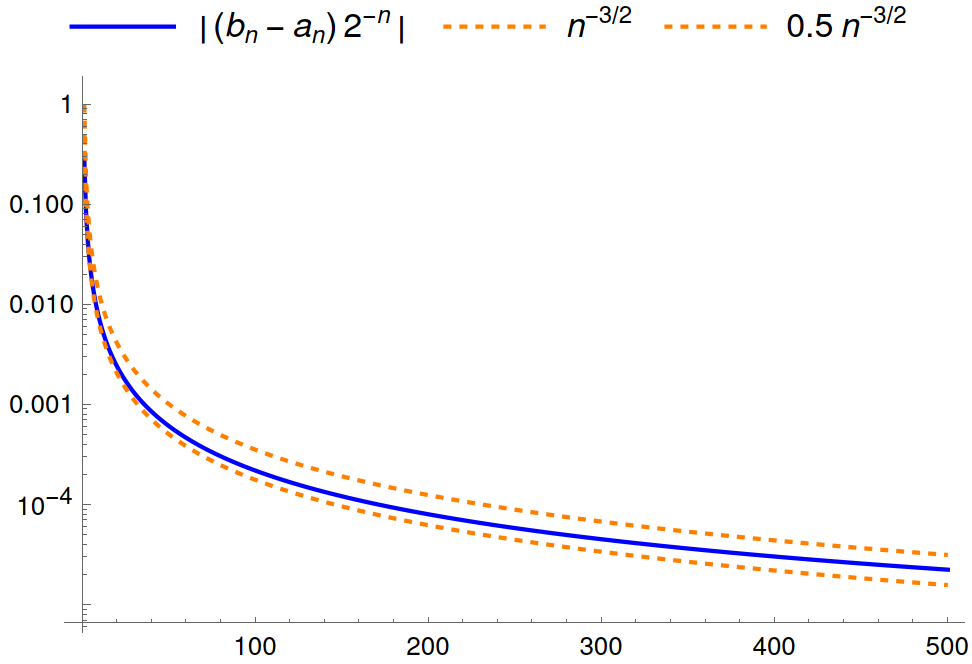The final, and most difficult, step is to see that the variance is $|b_n-a_n|\sim E\cdot n^{-3/2}\cdot 2^n,E\in\mathbb{R}_{>0}$. 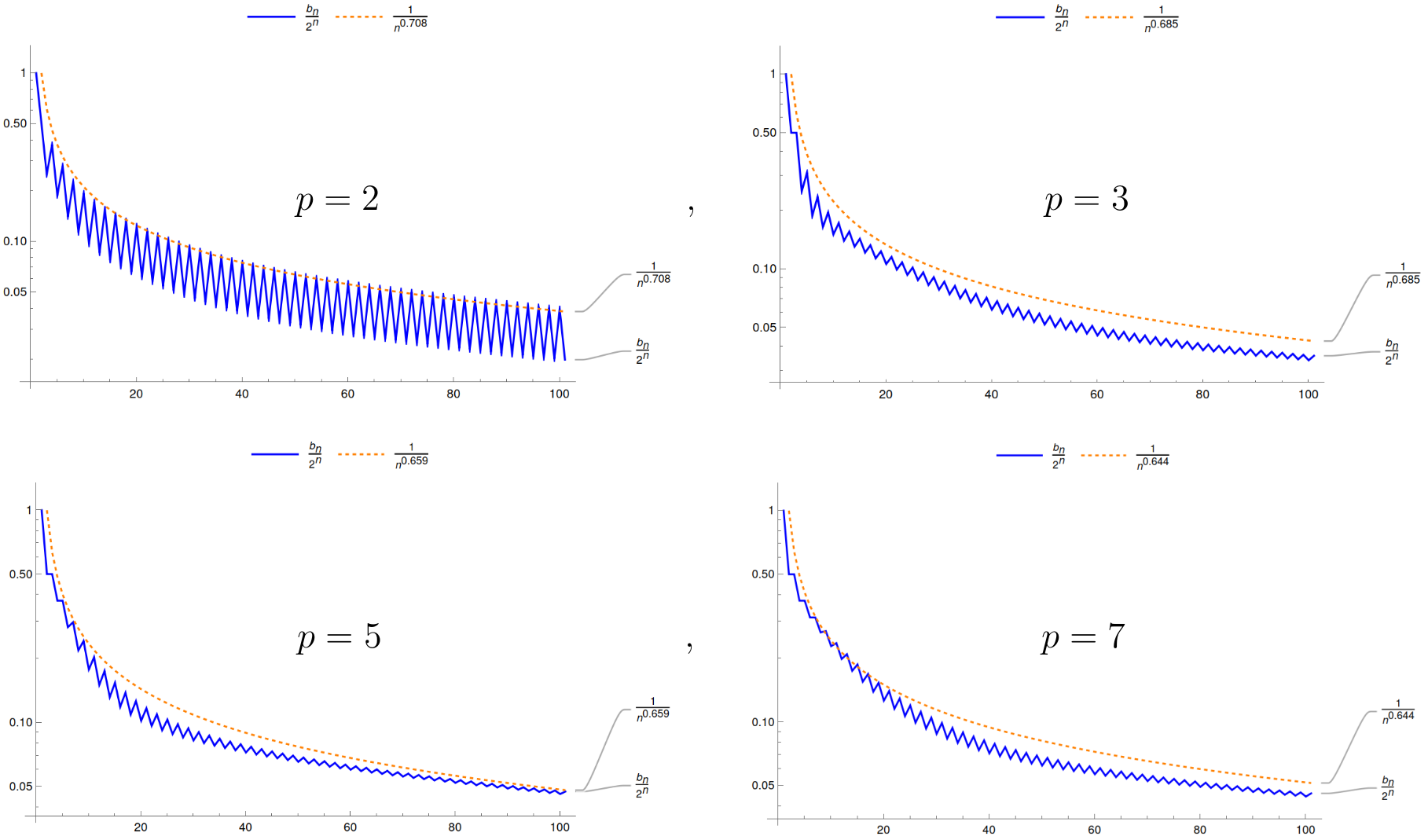The plots are:

This paper addresses the same type of questions for the prime characteristic version of the above. Specifically, for the algebraic group $G=\mathrm{SL}_{2}(\bar{\mathbb{F}}_p)$ and its vector representation $\bar{\mathbb{F}}_p^2$ we proved that the Ansatz above is valid and computed $a=-1+\tfrac{1}{2}\log_{p}\tfrac{p+1}{2}$ and $a'=\log_p(2p-1)$.
Our main tools are, on the algebraic side, tilting modules, and, on the analytic side, the theory of Mahler functions and Tauberian theory. Concretely, tilting modules form a well-studied class of modules of reductive groups, and as will be made more precise below, we intend for these modules to take over the role that projective modules play for finite groups. On the other hand, Mahler functions are functions that satisfy functional equations describing fractal behavior and which have well-studied asymptotics at their singularities. Tauberian theory in turn allows us to analyze growth rates of Taylor coefficients in terms of singularities.
The following picture underline our results: