Data

• Title: Categorification and applications in topology and representation theory
• Author: Daniel Tubbenhauer
• Status: published online by Universität Göttingen, Univ., Diss., 2013, DISS 2013 B 9481. Last update: Wed, 3 Jul 2013 13:43:42 GMT
• ArXiv link: http://arxiv.org/abs/1307.1011
• ArXiv version = 0.99 published version
• LaTex Beamer presentation: Slides1

Abstract

This thesis splits into two major parts. The connection between the two parts is the notion of “categorification” which we shortly explain/recall in the introduction.
In the first part of this thesis we extend Bar-Natan's cobordism based categorification of the Jones polynomial to virtual links. Our topological complex allows a direct extension of the classical Khovanov complex (h=t=0), the variant of Lee (h=0,t=1) and other classical link homologies. We show that our construction allows, over rings of characteristic 2, extensions with no classical analogon, e.g. Bar-Natan's \(\mathbb{Z}/2\mathbb{Z}\)-link homology can be extended in two non-equivalent ways.
Our construction is computable in the sense that one can write a computer program to perform calculations, e.g. we have written a MATHEMATICA based program.
Moreover, we give a classification of all unoriented TQFTs which can be used to define virtual link homologies from our topological construction. Furthermore, we prove that our extension is combinatorial and has semi-local properties. We use the semi-local properties to prove an application, i.e. we give a discussion of Lee's degeneration of virtual homology.
In the second part of this thesis (which is based on joint work with Mackaay and Pan) we use Kuperberg's \(\mathfrak{sl}_3\) webs and Khovanov's \(\mathfrak{sl}_3\) foams to define a new algebra \(K_S\), which we call the \(\mathfrak{sl}_3\) web algebra. It is the \(\mathfrak{sl}_3\) analogue of Khovanov's arc algebra \(H_n\).
We prove that \(K_S\) is a graded symmetric Frobenius algebra. Furthermore, we categorify an instance of q-skew Howe duality, which allows us to prove that \(K_S\) is Morita equivalent to a certain cyclotomic KLR-algebra. This allows us to determine the split Grothendieck group \(K^{\oplus}_0(K_S)\), to show that its center is isomorphic to the cohomology ring of a certain Spaltenstein variety, and to prove that $K_S$ is a graded cellular algebra.

A few extra words

Forced to reduce the thesis to one sentence, the author would choose:

The basic idea can be seen as follows. Take a “set-based” structure S and try to find a “category-based” structure \(\mathcal{C}\) such that S is just a shadow of the category \(\mathcal{C}\). If the category \(\mathcal{C}\) is chosen in a “good” way, then one has an explanation of facts about the structure S in a categorical language, that is certain facts in S can be explained as special instances of natural constructions.
As an example, consider the following categorification of the integers \(S=\mathbb{Z}\). We take \(\mathcal C=\)FinVec\({}_K\) for a fixed field k. We observe that \(K_0(\mathcal C)=\mathbb{Z}\). But a lot of information is lost from \(\mathcal{C}\) to \(K_0(\mathcal C)=\mathbb{Z}\), e.g. the first allows us to say how two vector spaces are isomorphic (think about non-trivial isomorphisms).
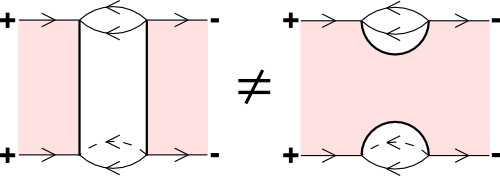
In our context this “richer structure” can e.g. be occur in the following example. A web, e.g. the bottom and top boundary of the figure below, can be seen as an intertwiner between tensors of certain representation of \(U_q(\mathfrak{sl}_3)\), denote by \(V_+\) and \(V_-\). In the figure below we show one web between \(V_+\) and \(V_-\) (both as short hand notation just denoted + and -). In the picture there is only one web, but a foam (a type of singular cobordism) can tell “how” they are equal.