Data
- Title: Diagram categories for \(\textbf{U}_q\)-tilting modules at roots of unity
- Authors: Henning Haahr Andersen and Daniel Tubbenhauer
- Status: Transform. Groups 22 (2017), no. 1, 29-89. Last update: Thu, 31 Dec 2015 09:24:33 GMT
- ArXiv link: http://arxiv.org/abs/1409.2799
- ArXiv version = 0.99 published version
- LaTex Beamer presentation: Slides1, Slides2, Slides3
Abstract
In this paper we give a diagrammatic category (inspired by Elias' dihedral cathedral) that
is a diagrammatic presentation of the category of \(\textbf{U}_q(\mathfrak{sl}_2)\)-tilting
modules \(\mathfrak{T}\) for q being an l-th root of
unity. Moreover, we, following an approach of Soergel and Stroppel, introduce a grading turning \(\mathfrak{T}\) into
a graded category \(\mathfrak{T}^{\mathrm{gr}}\). This grading is a purely “root of unity” phenomena
and might lead to new insights about the link, tangle and 3-manifold invariants deduced from \(\mathfrak{T}\).
In addition, we also give a diagrammatic category for the (now graded) projective endofunctors \(p\textbf{Endo}(\mathfrak{T}^{\mathrm{gr}})\),
indicate how our results could generalize to \(\textbf{U}_q(\mathfrak{sl}_n)\) and maybe other types and recall/collect some “well-known”
facts to give a reasonably self-contained exposition.
A few extra words
Khovanov and Lauda have categorified \(\textbf{U}_v(\mathfrak{sl}_k)\) (for an indeterminate v).
Their approach was to use diagrammatic categorification: They defined a certain 2-category \(\mathcal U(\mathfrak{sl}_k)\)
consisting of a certain type of so-called string diagrams whose (split) Grothendieck group \(K_0^{\oplus}(\mathcal U(\mathfrak{sl}_k))\) (roughly)
gives the quantum group back. One of their main observations was that the E's and F's of the quantum group
behave like biadjoint(!) induction and restriction functors on certain categories. It is “folklore knowledge” that biadjoint functors have a “built-in
topology” since, roughly, biadjointness means that we can straighten out diagrams.
Their program of diagrammatic categorification has turned out to be very fruitful: Using diagrams and manipulate them topological
and combinatorial has already led to seminal results in various contexts. The reader unfamiliar with diagrammatics may think of their
usefulness in the same way as a good notation clears ones understanding of a problem. Moreover, it is a “low-tech” approach an can be done explicitly.
Thus, since certain functors on \(\mathfrak{T}\) (for the experts: the translation functors)
have this biadjoint property, it was only natural to look for a diagram category that describes the tilting story. That is
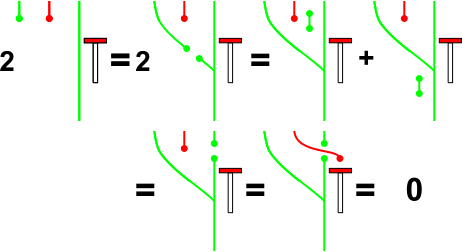
in fact what we do in the paper. Below there is such a diagram: Some manipulations are combinatorial and some are topological
(and, at least in the opinion of the authors, way simpler that to work with fancy intertwiners and higher stuff connected to them).