Data
- Title: The Blanchet-Khovanov algebras
- Authors: Michael Ehrig, Catharina Stroppel and Daniel Tubbenhauer
- Status: Categorification and Higher Representation Theory, 183-226, Contemp. Math., 683, Amer. Math. Soc., Providence, RI, 2017. Last update: Thu, 26 Jan 2017 07:12:18 EST
- ArXiv link: http://arxiv.org/abs/1510.04884
- ArXiv version = 0.99 published version
- LaTex Beamer presentation: Slides1, Slides2
Abstract
Blanchet introduced certain singular cobordisms to fix the functoriality of Khovanov homology. In this paper we introduce graded algebras consisting of such singular cobordisms à la Blanchet. As the main result we give algebraic versions of these algebras using the combinatorics of arc diagrams.
A few extra words
For an arbitrary field \(\mathbb{K}\) we consider the
\(\mathfrak{sl}_{2}\)-web algebra .
This is a graded \(\mathbb{K}\)-algebra which
naturally appears as an algebra of singular
cobordisms. In particular, it is of topological origin.
The underlying category of singular cobordisms was used
by Blanchet to fix the functoriality of Khovanov homology.
Its objects are certain trivalent graphs and its
morphisms are singular cobordisms whose boundary are such trivalent graphs.
We call these singular cobordisms \(\mathfrak{sl}_{2}\)-foams.
An example of such foams is provided by the following relation
which holds in the \(\mathbb{K}\)-linear 2-category
consisting of these singular cobordisms:
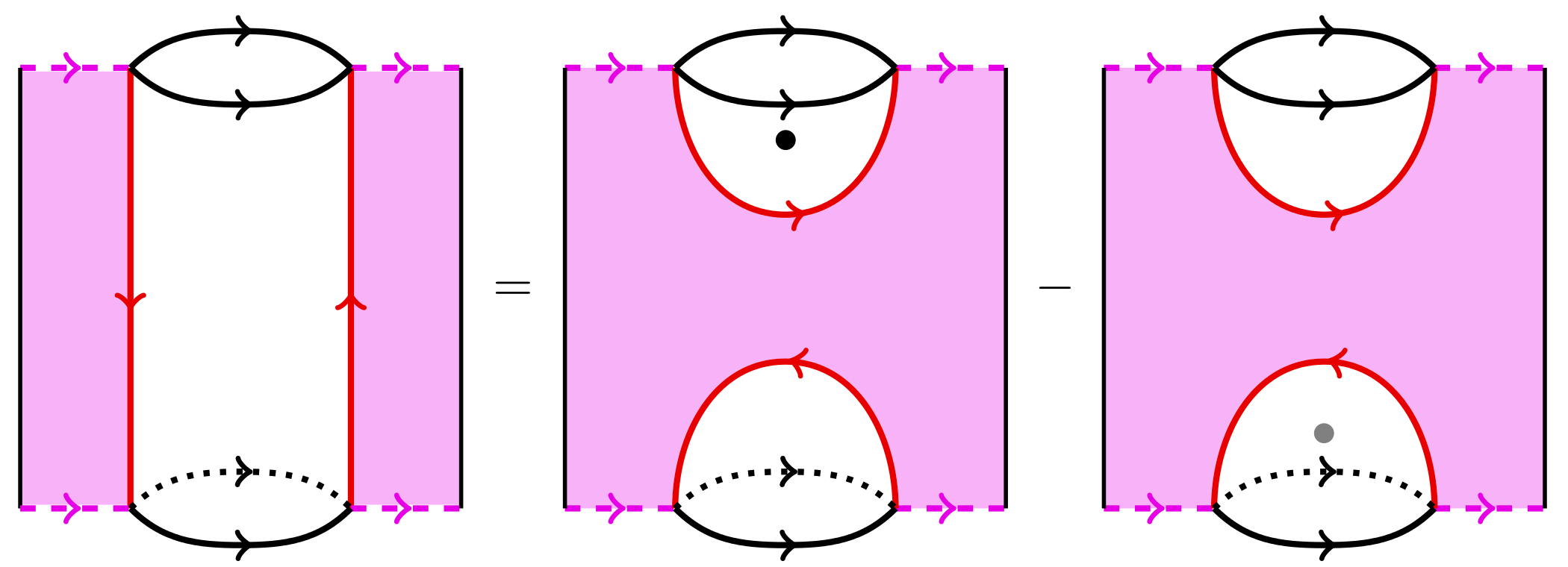
This relation is called the neck cutting relation and plays a crucial part in the whole story.
Working with such foams is topolocially motivated, but hard in practice. In this paper we give an algebraic counterpart of . This provides a direct link between the topological and the algebraic point of view. As a consequence, computations (which are hard to do in practice on the topological side) can be done on the algebraic side, whereas the associativity (a non-trivial fact on the algebraic side) is clear from the topological point of view.